Reflection
우리는 모든 물체는 정반사와 난반사가 동시에 일어나고 반사 된 빛이 우리 눈에 들어와서 물체를 인식 할 수 있다는 원리를 이해하고 있습니다. 이번 포스트에서는 반사(Reflection)를 구현해보도록 합시다.
정반사율이 높은 적당한 오브젝트를 하나 구합니다. 저는 금속 헬름 모델링을 예시로 삼았습니다.
헬멧에 반사시킬 스카이박스용 큐브맵을 하나 구합니다.
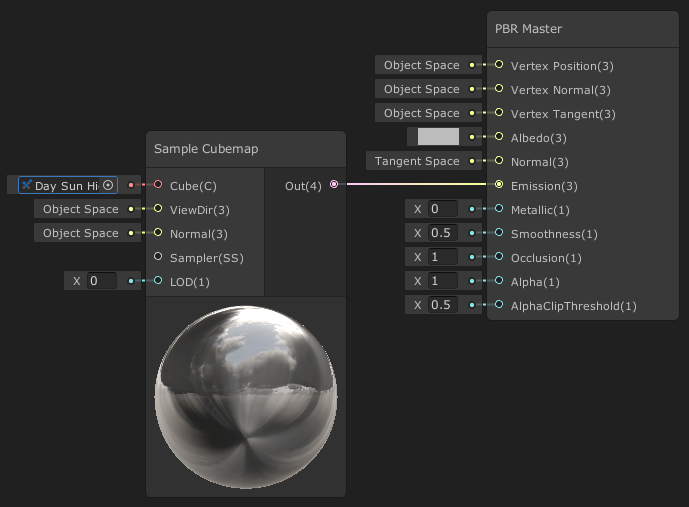
큐브맵을 이미션(Emission)에 연결하면 순수한 반사 만 관측할 수 있습니다.
사실 엄밀한 의미의 반사는 아닙니다. 이것은 스카이박스 텍스쳐를 오브젝트 표면에 매핑한 것일 뿐입니다. 주변에 배치된 오브젝트는 반사되지 않습니다.
샘플러 큐브맵이 오브젝트 표면에 반사되기 위해서는 기존 오브젝트의 UV 데이터가 아닌 리플렉션 벡터를 UV로 사용합니다. 리플렉션 벡터를 연산하기 위해 뷰 디렉션과 오브젝트 스페이스 노말이 필요합니다.
노말 맵이 적용된 반사를 구현하기 위해 위와 같이 트랜스폼 노드로 Object 스페이스로 변환하고 연결해줍니다.
노말 맵이 적용되어 표면이 울퉁불퉁하고 마모된 느낌을 받습니다.
다음은 헬름에서 반사가 일어나지 않는 재질들을 분리시켜봅시다.
마스킹 텍스처를 곱합니다. 반사가 일어날 부분은 1 일어나지 않는 부분은 0을 곱해서 반사를 수정해줍니다.
PBR 마스터 노드에 알베도 텍스처를 연결합니다.
하지만 PBR 마스터 노드의 공식대로 계산하게 되면 물리적으로 오류가 생깁니다. 알베도 + 이미션이 되어 1을 넘는 색을 가지게 되기 때문입니다. 따라서 알베도 텍스처도 값을 반전한 마스킹 텍스처와 곱해주어야 합니다.
제대로 스카이박스 반사가 동작합니다. 같은 원리로다음은 잔잔한 호수와 강물 같은 수면의 반사를 표현해봅시다.
먼저 언릿 마스터 노드에서 Plane에 반사 시킬 큐브맵을 넣습니다.
각기 다른 방향으로 흐르는 노말맵 두개를 더해준 뒤, 절반으로 나눠주면 자연스레 흐르는 액체가 됩니다.
하지만 아직 물이라고 부르기에는 부족한 것이 많습니다. 하늘을 100% 반사 하기 때문에 지금은 마치 수은같은 유체 금속의 성질에 가깝습니다.
알파를 켜고 프레넬을 추가합니다. 물의 투명함이 뷰 벡터(카메라의 각도)에 영향을 받게 만들어 뷰 벡터가 물 표면과 수직에 가까울수록 투명하고 평행에 가까울수록 반사하도록 합니다.
퐁 리플렉션 모델 공식으로 태양의 스페큘러도 추가해줍니다. 하지만 현재 물의 표면은 알파가 적용되고 있기 때문에 실제 값보다 매우 약해진 스페큘러입니다. 제대로 된 스페큘러를 구현해 봅시다.
먼저 햇빛이 스페큘러에 적용되도록 조명의 색을 곱해줍니다.
초록색 네모 부분의 노드에서 큐브맵에 스페큘러를 더합니다. 여기서 의도적으로 1이상의 값을 생기게 해서 HDR이 되게합니다. 스페큘러 값에 임의의 숫자를 곱해서 조절해 줄 수 있습니다.
파란색 네모 부분의 노드에서 스페큘러를 그대로 프레넬에 더해버려서 마스크로 적용합니다. 즉 스페큘러가 있는 부분은 투명하지 않게 됩니다.
포스트 프로세스에서 Bloom 을 적용하면 이렇게 됩니다.
이번에는 버텍스 포지션을 조절하여 노말 뿐만 아니라 실제로 물의 표면이 움직이도록 해보겠습니다.
UV의 R채널 그라데이션을 오브젝트 포지션의 y축에 더하면 어떻게 될까요?
Plane이 한 쪽으로 기울어지게 됩니다.
균일한 0~1 그라데이션이 포지션에 더해졌으니 위와 같이 기울어지게 된 것입니다.
저희는 이제 그라데이션 연산으로 버텍스를 일정하게 기울일 수 있다는 것을 알았습니다. 다음은 물결 모양으로 만들어봅시다.
abs(Color *2 -1)
이렇게 0~1 그라데이션에 2를 곱하고 -1으로 줄인 뒤 절댓값을 구하면 좌우가 1이고 중간이 0인 그라데이션이 나옵니다.
노드로 구현하면 위와 같이 V 모양으로 버텍스 포지션이 움직입니다. 각진 부분을 보간해보도록 합시다.
y = Sin(θ*|β|+γ)*α+δ
삼각함수중 가장 기본적인 파동 형태를 가진 Sine 함수로 제어해보도록 합시다.
(읽기 전에 알아둬야할 수학 용어들)
위의 그래프에서 알 수 있듯이 θ 값은 삼각형의 각도 값이며 저희는 각도 대신 그라데이션 값을 넣을 것입니다.
중학교 수학시간에 이차함수에 대해 공부했듯이 Sine 함수 그래프의 수직 수평이동은 물론이고 파장, 진폭, 주기를 결정할 수 있습니다.
α 알파 값은 진폭을 늘리고 줄일 수 있습니다.
β 베타 값은 주기를 늘리고 줄일 수 있습니다.
γ 감마 값은 그래프를 수평이동 합니다.
δ 델타 값은 그래프를 수직이동 합니다.
중요한 점은 현재 그라데이션은 0과 1사이의 값이기 때문에 한 번의 파장이 완성되려면 2π의 근사치 값까지 확장해줘야 합니다. 그래서 Sine 함수로 연산하기 전에 곱셈으로 대충 6.28 쯤 곱해줍시다.
하지만 Plane의 폴리곤은 버텍스의 숫자가 부족해서 저희가 원하는 만큼 부드럽지 않고 위와 같은 결과가 나옵니다. 그래서 알파α 값으로 진폭을 줄여 줍시다.
그나마 자연스럽게 변했습니다. 파장을 만들었으니 그래프 전체가 끊임 없이 수평이동 하도록 감마γ 값을 Time 함수로 만들어줍시다.
중요한 포인트는 감마 값을 Time 함수로 두게 되면 절대값 abs 함수에 의해 그래프가 양방향으로 수평이동하게 됩니다.
Time 함수는 Scene이 시작된 이후 흐른 시간을 초 단위로 소수점 이하의 값을 유지하면서 반환합니다. 즉 타임 함수를 더한다는 것은 영원히 값이 증가한다는 것입니다.
값을 Sine 함수에 대입하면 2π 주기마다 파장을 이루게 되는 것입니다.
다음 포스트에서 굴절을 추가하여 보겠습니다.
Comments