(UnityShader) 09 Fragment Advanced : Texcoord rotation
float2x2(cosθ, -sinθ, sinθ, cosθ)
저희는 지난 포스트에서 위와 같이 회전 행렬을 유도했습니다. 이번에는 회전행렬을 이용해 texcoord를 원하는 각도만큼 회전 시키는 기능을 fragment 쉐이더로 구현 할 것입니다.
그러기 위해서는 앞서 말한 '원하는 각도(Degree)'에 대한 정확한 정의와 '라디안(Radian)' 개념에 대하여 제대로 알고 있어야 합니다.
(회전과 각도)
저희가 유니티에서 어떤 오브젝트를 회전시킬 때, 회전을 시작하기 전과 완전히 똑같아진 상태의 각도는 360˚ (Degree) 입니다. 어떤 물체가 완벽히 한 바퀴를 돌았을 때의 각도가 360도라고 수학자들이 약속하고 국제 표준 단위로 정한 것이지요. 우리말로는 '60분법'이라고 부릅니다.
(라디안의 정의)
하지만 게임 엔진에서 수학으로 각도를 계산할 때는 라디안(우리말로는 호도법)이라는 방식을 사용합니다. 왜냐하면 쉐이더 프로그래밍 언어는 각도 단위를 받아들이지 않기 때문입니다.
여기 반지름이 1인 도형 원이 있습니다. 원의 각도는 360˚ 입니다. 원의 둘레 길이는 항상 반지름의 2π 배 길이를 가진다는 수학적으로 증명된 사실이 있지요.
저희는 이러한 원을 임의의 각도(θ)를 가진 부채꼴으로 잘랐습니다. 그런데 우연히도 부채꼴 호의 길이 또한 반지름과 같은 값인 '1'입니다.
수학자들은 호의 길이가 반지름의 길이와 같다는 조건을 만족하는 부채꼴의 각도를 1 radian(줄여서 rad로 표기)라고 정의하였습니다.
너무 수학적인 이야기들이 많이 나왔으니 저희 초보 아티스트들을 위하여 최대한 쉽게 차근차근 정리 해보겠습니다.
원의 반지름이 r(radius) 이라면, 원의 둘레 길이는 2π 곱하기 r 입니다.
부채꼴의 각도가 ϕ 라면, 0~360 사이의 값이니, ϕ 나누기 360 으로 표기할 수 있습니다.
따라서 저희는 원의 반지름도 알고 있고 부채꼴의 각도도 알고 있으니 부채꼴 호의 길이를 계산 할 수 있습니다.
(부채꼴 호와 반지름의 관계)
부채꼴 호의 길이가 l 이라면, 아래와 같은 식이 성립합니다.
l(길이) = 2π * r(반지름) * ϕ/360
= π * ϕ/180 * r
2를 곱해서 360은 180이 되고,
= π * ϕ/180 = l/r
양변을 r으로 나누고 뒤집으면 정리가 끝납니다.
따라서 각도 값이 곧 호의 길이와 반지름의 비(l/r)가 되기 때문에 각도 단위(degree)를 사용하지 않고 float 데이터로 나타낼 수 있게 되었습니다. 코드로 각도 단위를 표기할 수 없다는 문제점을 해결하고 게임 엔진에서 쉐이더 프로그래밍 언어로 사용할 수 있는 상태가 된 것입니다.
(비례식. 부채꼴 호의 길이와 반지름의 길이가 같다면 위의 식이 성립한다)
다른 방법으로는 비례식을 세우고, 외항과 내항의 곱은 같다는 원리를 이용해서 1 radian 을 정의 해줄 수도 있습니다.
식을 보기 좋게 정리했습니다. 저희는 이제 라디안과 각도를 위와 같이 용도에 따라 서로 변환 해줄 수 있게 되었습니다. 그렇다면 무한소수인 원주율(π) 값은 어떻게 써줘야 할까요?
(#include "UnityCG.cginc")
π(파이)는 UnityCG.cginc 속에 근사치로 소수점 아래 11번째 자리까지 정의 되어 있습니다. 저희는 UNITY_PI 변수를 쓰면 됩니다. 필요한 정보는 다 구했으니 드디어 대망의 코딩입니다.
_Rotate ("Degree", Range(0,360)) = 0
프로퍼티는 저희가 직관적으로 사용할 수 있게 60분법으로 만듭니다. 쉐이더 내부에서 라디안 방식으로 변환 하여 사용할 것입니다. Range 0~360으로 변수를 설정해줍시다.
변환 과정이 생각보다 길어서 커스텀 펑션으로 모듈화 해서 사용할 것입니다. input으로 Maintex의 texcoord 데이터를 받기 위해 float2 uv를 써주고, float degrees로 각도 값을 받습니다.
float Degree2Rad = UNITY_PI * 2 / 360;
float rotationRadians = degrees * Degree2Rad;
원주율* 2/360(1/180으로 해도 무방함)을 각도 값에 곱하여 라디안으로 변환합니다.
float c = cos(rotationRadians); float s = sin(rotationRadians); float2x2 rotateMatrix = float2x2(c, -s, s, c); uv = mul(uv, rotateMatrix);
코사인세타(cosθ), 사인세타(sinθ), 회전 행렬을 선언해줍시다. 그리고 Texcoord * Matrix 순서로 행렬곱 해줍시다.
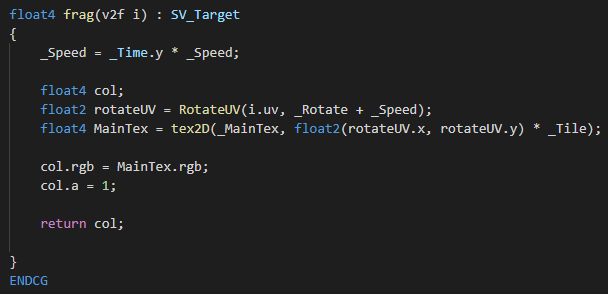
메인텍스처의 uv에 함수를 적용해줍니다. 저는 time 함수로 자동으로 회전할 수도 있게끔 했습니다.
그런데 결과가 이상합니다. 정상적으로 작동하긴 하지만 텍스처의 왼쪽 아래를 기준으로 회전합니다. 텍스처의 중앙에서 회전하게 하려면 어떻게 해야 할까요? 아래로 스크롤을 내리기 전에 잠시 생각 해보도록 합시다.
uv -= 0.5;
uv = mul(uv, rotateMatrix);
OpenGL 기준 UV의 왼쪽 아래가 (0,0)이기 때문에 uv의 (0,0) 원점 좌표를 기준으로 회전하고 있었습니다.
따라서 정답은 회전행렬을 곱하기 전에 uv를 -0.5만큼 이동시키는 것입니다. 그러면 (0.5,0.5)였던 부분이 원점(0,0)이 되서 회전하는 것이지요.
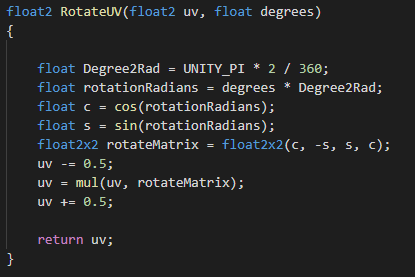
uv -= 0.5; uv = mul(uv, rotateMatrix); uv += 0.5;
행렬곱 이후에 0.5를 더해서 uv를 원래대로 만들어줍니다. 회전 행렬의 기준점만 변경한 것이 되는 것입니다.
완성입니다. 끝까지 읽어주셔서 감사합니다.